扩散模块的特征
总体设计
-
合金成分、相体积分数和相成分随时间的变化图
-
热历史、边界条件和几何的多重选择
-
第二相固溶,碳化与脱碳,均匀化热处理,扩散相变以及扩散偶等应用
动力学模型
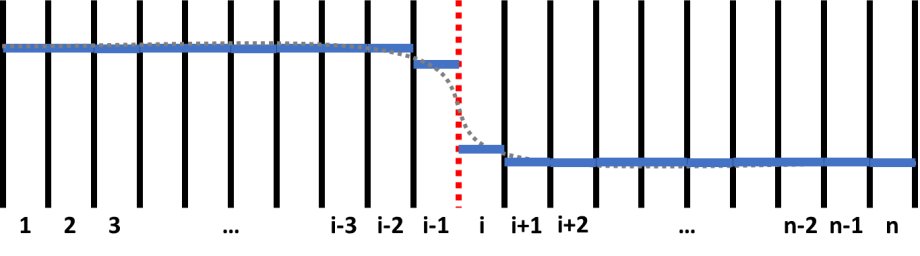
图 1 所示为一扩散偶中的成分分布图。在此模拟中,样品划分为等宽度的网格。数字1、2、3、…、n表示第i个网格。黑色实线和红色虚线均代表网格界面,在第(i-1)个和第i个网格之间的红色虚线代表扩散偶界面的初始位置。网格间元素流量根据菲克第一定律计算。如图 1中的灰色虚线为成分分布,蓝色实线表示的是其离散分布示意图。在完成成分计算后,每个网格的化学势,迁移率,相平衡和相关性质都将更新。
流量模型
每个网格的成分由网格间的流量决定,基于绝对反应速率理论[1941Gla]计算获得。在格子固定的参考系,流量为:
|
|
(1) |
其中是第i和i+1个网格之间的第k个元素的流量,
是k元素的有效迁移率,R是气体常数,T是温度,单位为K,
为摩尔体积,
代表网格厚度,多数情况下由网格平均尺寸计算得到,
和
分别是元素 k 在第i和i+1个网格的摩尔分数,
是元素k在网格i和i+1之间的化学势差值。sinh是双曲正弦函数。为计算方便,在体积确定的参考系中得到成分分布图,代替元素的流量通量转换为
。
然后根据菲克第二定律更新每个网格上元素k的数量():
|
|
(2) |
其中单位法向量从网格向外指向。
[1941Gla] S. Glasstone et al., “The theory of rate processes”, New York, NY: McGraw-Hill; 1941.